I had a little bit of dread around my last post, on algorithms and complexity because while I have a moderate handle on these concepts, I’m by no means an expert. My greatest fear was that someone who really knew the material would read it, scoff, and hammer me publicly. And sure enough, in no time I had an email, for some reason anonymous, telling me I’d gotten the O-factors wrong; that the original “naive” algorithm was in fact O(n^2), and that my improved algorithm was plain old O(n).
Before too long, another email revealed that the comment was from my college roommate and colleague Thomas Andrews, who taught me most of what I know about algorithmic complexity. At least the hammer is from a friendly quarter! Thomas had a number of observations on the discussion, which I’ll try to reproduce here, along with some additional implementations and analysis. None of this alters the essential point that divide-and-conquer is a much better approach than iteration — but the discussion shows shows that even among algorithms that are of theoretically comparable efficiency, there can be important real-world differences.
Thomas’ first point was that I hadn’t really analyzed every aspect of algorithmic complexity. My discussion really just focused on the needed number of recursions. My point was that the naive algorithm requires n recursions, while the divide-and-conquer approach requires about log(n) recursions. So from that standpoint, the n-vs-log(n) contrast was correct.
However, function calls are not the only cost involved in these methods. The calls also allocate memory, and move data around in memory to a greater or lesser extent. Thomas offered a basic point: “You can’t create a string of length n in less than O(n) time.” Why not, you might ask? Because the act of creating the string involves filling n memory locations with data. Each of those write operations “counts” in the assessment of algorithmic complexity. In addition, you must count any intermediate copying or writing of data you do along the way needs to be counted as well.
“Wait a minute,” you might reply. “Computers often write data in chunks. If a processor is writing eight or 16 bytes of data at once, that memory would be filled in n/8 or n/16 operations. That’s faster than O(n)!” That sounds right, but in the analysis of algorithmic complexity, n/8 and n/16 are really just the same as n. In other words, O(n) = O(kn) where k is any constant (in this case the constants are 1/8 and 1/16). The reason is that for any specific k, n can always grow big enough to reduce k to insignificance. So altering running time by a constant factor can’t change the O-ranking of an algorithm. It can, though, have important practical consequences, as we’ll see in a bit.
Thomas went on to point out that, when you take the likely memory manipulations into account, the original naive algorithm is in fact O(n^2), since you are copying the current state of the string (writing it to a new memory location) with each recursive call. So you have n recursive calls, each with O(n) write operations, for a total complexity of O(n^2).
“But wait,” you might say again, “that’s not fair. You’re not copying n characters each time. You only copy n characters at the very end. You start by copying 1 character, then 2, then 3, etc. So doesn’t this analysis overstate the cost?” No, it doesn’t. It’s true that the average copy operation, as the loop iterates from 1 to n repeats, is about n/2 copies. But remember that O(n/2) is identical to O(n), since 2 is a constant.
So as a matter of fact my approach reduced the complexity from O(n^2), which is a very inefficient level, to O(n), which probably didn’t deserve the “meh” I gave it in the earlier post. We’ll take a look at how O(n^2) and O(n) look side by side later on.
Thomas went on to make another important point. “You can avoid doing the logarithm calculation, which is actually costly if the number of repetitions is small.” Thomas then offered an alternate implementation, which I’ll get to in a minute. But why did he say that the logarithm calculations were “costly”? Thomas explained that “In general, most of the transcendental functions (trig functions, e^x, log) are slow because they are computed using series, which can involve a lot of floating point arithmetic, which is always much slower than integer math.”
I thought it was time to take a look at how this played out in reality. This gets to one of the key points of this post — analysis of complexity only gets you so far. Though a “better” algorithm will outperform a “worse” algorithm in the general case (which is mostly reached by making n large enough), there can be important differences in specific cases. Here Thomas was warning me that I was using a complex math function that might make the picture different for small numbers of repetitions. In fact, I was compounding the problem. My exponentiation function, which FileMaker doesn’t have natively, was implemented via additional log calculations.
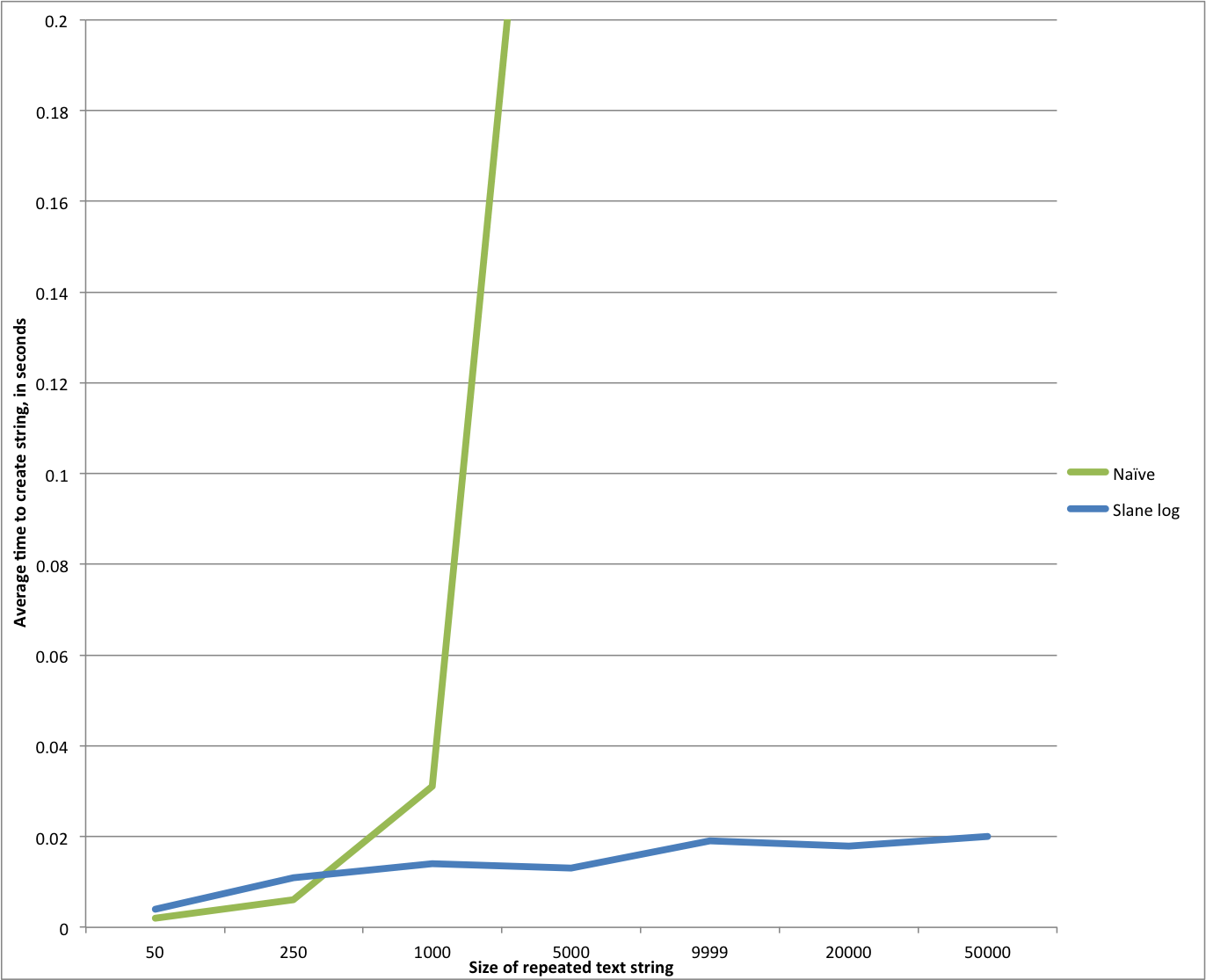
- Thomas is clearly correct that the original algorithm is O(n^2). The growth in running time of the original algorithm follows a clear n^2 curve path.
- The difference between an O(n^2) algorithm and an O(n) algorithm is very clear. The running time of the original algorithm after a certain point diverges hugely from the divide-and-conquer method. Going from 255 to 1000 repetitions at O(n^2) makes the run time go up fivefold, while going from from 1000 to 5000 repetitions increases the runtime an additional tenfold. By contrast, from 250 to 500 repetitions the divide-and-conquer approach adds 25% to the run time, and actually appears to go DOWN slightly from 1000 to 5000 repetitions. Going to 10,000 and 20,000 repetitions adds about another 50% to the run time. From 20,000 to 50,000 repetitions adds maybe another 10%. The divide-and-conquer algorithm is 60 times faster than the iterative algorithm at 10,000 repetitions, and from there moves easily to 20K and 50K, numbers that the iterative algorithm can’t achieve at all without further tuning — and even if it did so, it would be running literally thousands of times slower than the O(n) technique.
- The O(n) technique is actually slower than the O(n^2) technique for small n.
I tried to slip that last item in there without much fanfare. That’s right — for n less than about 300 or 400, my fancy divide and conquer technique is actually SLOWER than the algorithm I’ve been castigating as “naive.” Heh, whoops! What’s up there? It’s hard to know for certain, but very likely be tied to Thomas’ remark that the expense of the log-based approach might be telling for small n. Turns out he was right on the money, as he was about the polynomial growth rate of the first algorithm.
If these were the only two techniques we had available, we could stop there and use this as an illustration that things are rarely as nice in the real world as on paper. Empirical testing here shows that the O(n) algorithm is massively faster than the naive algorithm for large n, but if we only had these two approaches, we’d be well advised to code a hybrid routine that used iteration for n up to about 400, and the “flatter” algorithm for higher n (in other words, based on the value of n, choose one method or the other). After all, a majority of uses of the function might well be for n under 400. This is a classic example of the need to test empirically and optimize based on your actual findings.
But are there other approaches? We know that the log functions are costly — can they be avoided? As I mentioned, Thomas had a better proposal, one that avoids transcendental functions and uses the “exponentiation by squaring” approach he mentions in a comment on the first post. Here’s his function and his analysis:
RepeatTA( text; numReps )
Let( [ halfNum = Floor( numReps / 2 );
halfRepeats = Case( numReps > 1;
RepeatTA( text; halfNum ); "Ignored" );
remainderText = Case( numReps = 2 * halfNum; "" ; text );
result = Case( numReps = 0; "";
numReps = 1; text;
remainderText & halfRepeats & halfRepeats )
];
result
)This is related to an algorithm called “Exponentiation by Squaring”). Essentially, if you think of “append two strings” as a binary operation, then this function is to appending as exponentiation is to multiplication. This still takes O(n) time, as I said, because you can’t build a string up in less time than the length of the resulting string.
A big hidden cost of the original algorithm is memory allocation. If text is M characters, then you are first allocating a block of 2M characters, then a block of 3M characters, then a block of 4M characters. You are always freeing up the memory when you are done with it, but bad things can happen when you allocate memory in this way – memory fragmentation – and you are essentially allocating up to O(MN^2) bytes of memory over the operation. The “Exponentiation by Squaring” algorithm allocates only O(MN) memory.
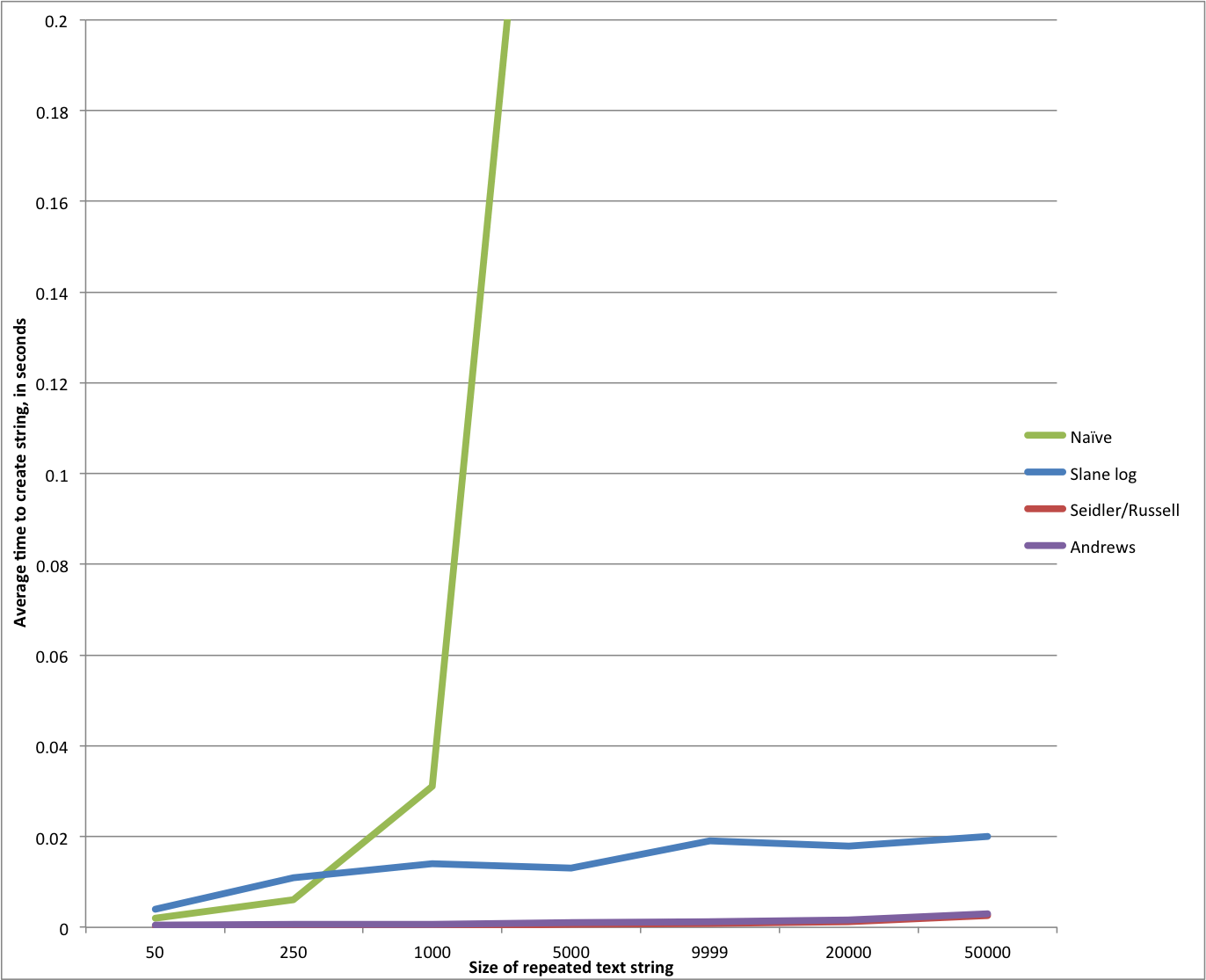
So how does this function do relative to my log-based algorithm? Much better — on average it’s about ten times as fast, which is enough to beat the naive algorithm handily even for the smallest n. Now, note that this function is not better than mine in the same way that both are better than the naive method: the performance gap between these O(n) algorithms and the naive O(n^2) algorithm grows over time, and eventually explodes, whereas Thomas’s method remains constantly about ten times faster than mine for all the data sizes I checked. But even though the two methods are approximately equally good, the RepeatTA function is empirically ten times better than mine.
So we’re done, right? Well, not quite.
When I first thought of how to do this, I thought of a simpler approach. It was still a double-based, divide-and-conquer approach, but my idea was, instead of doubling the string until I reached the largest power of 2 that was smaller than numReps, instead to reverse it, and double up to the smallest power of two larger than numReps. In other words, double the string until it’s too big, and then cut it back down to size somehow. A simple way to do that is with FileMaker’s Left() function. I had initially rejected this idea out of concern that running Left() on large strings would be inefficient. My evidence for this? Instinct and intuition, in other words, no evidence at all. In fact this method has already been posted on the Internet, and was also suggested in a comment on the first post.
Here’s what such a function looks like. It’s the simplest version yet:
RepeatWithLeft( text; numReps )
Case ( numReps > 2 ; RepeatWithLeft ( text & text ; numReps/2 ) ;
numReps > 0 ; Left ( text & text ; Round ( numReps * Length ( text ) ; 0 ) ) ;
)Very simple indeed. And how does it perform? It performs even slightly better than Thomas’ algorithm, approximately doubling its speed for smaller n. However, though the gap narrows as n grows larger, and might eventually close or cross over.
My point in mentioning this last case is both to give credit where it’s due, and to point out how wrongheaded was my initial instinct that Left() would be inefficient. In order to “improve” on it, I wrote an algorithm that used expensive transcendental functions. The only way to know how fast something is in the real world is to test it, period. I was certainly correct that a divide-and-conquer algorithm would wallop the O(n^2) algorithm in the long run, but as we can see, there was still room for huge real-world improvements in my, dare I say it, naive O(n) approach.
Great post.
Although I’m confused about why your function is not log(n). The act of creating the string may involve filling n memory locations, but the creating of the string happens log(n) times, not n times.
Hi Mislav:
Well, your question contains its own answer, in a way. Once you've filled n memory locations even once, you've already taken n time, so the algorithm is O(n) at best. Now, if we really needed to fill n locations log(n) times, then the algorithm would be O(nlogn). This is a pretty common efficiency class.
Imagine that the algorithm actually runs something like this. We first write one character to memory. Then we double it by writing one more directly after. Then we double again by writing two more after the first two, four more after the first 4 etc. The number of such operations is about log(n) [log base 2 of n to be more exact]. We write a total of n characters (a bit more, since this algorithm takes us over n). So the average number of characters written per loop is n/log(n). Now multiply that by the number of loops, log(n), and we get back to plain old n.